I have ten meters of mesh fence. I want to make two enclosures for my rabbits who can’t stand each other (they can share a wall). What is the shape and the area of the largest enclosure (in terms of area) I can build? Each rabbit needs to have access to the same area. The shape can be arbitrary (although it would be nice if it were continuous or smooth to some extent, and each area contiguous).
Examples:
A square of 2x2m, divided by a 2m wall. Area: 4 square meters
A circle of radius 1.21m, divided by a wall. Area: ~4.58 square meters.
Is it possible to do better?
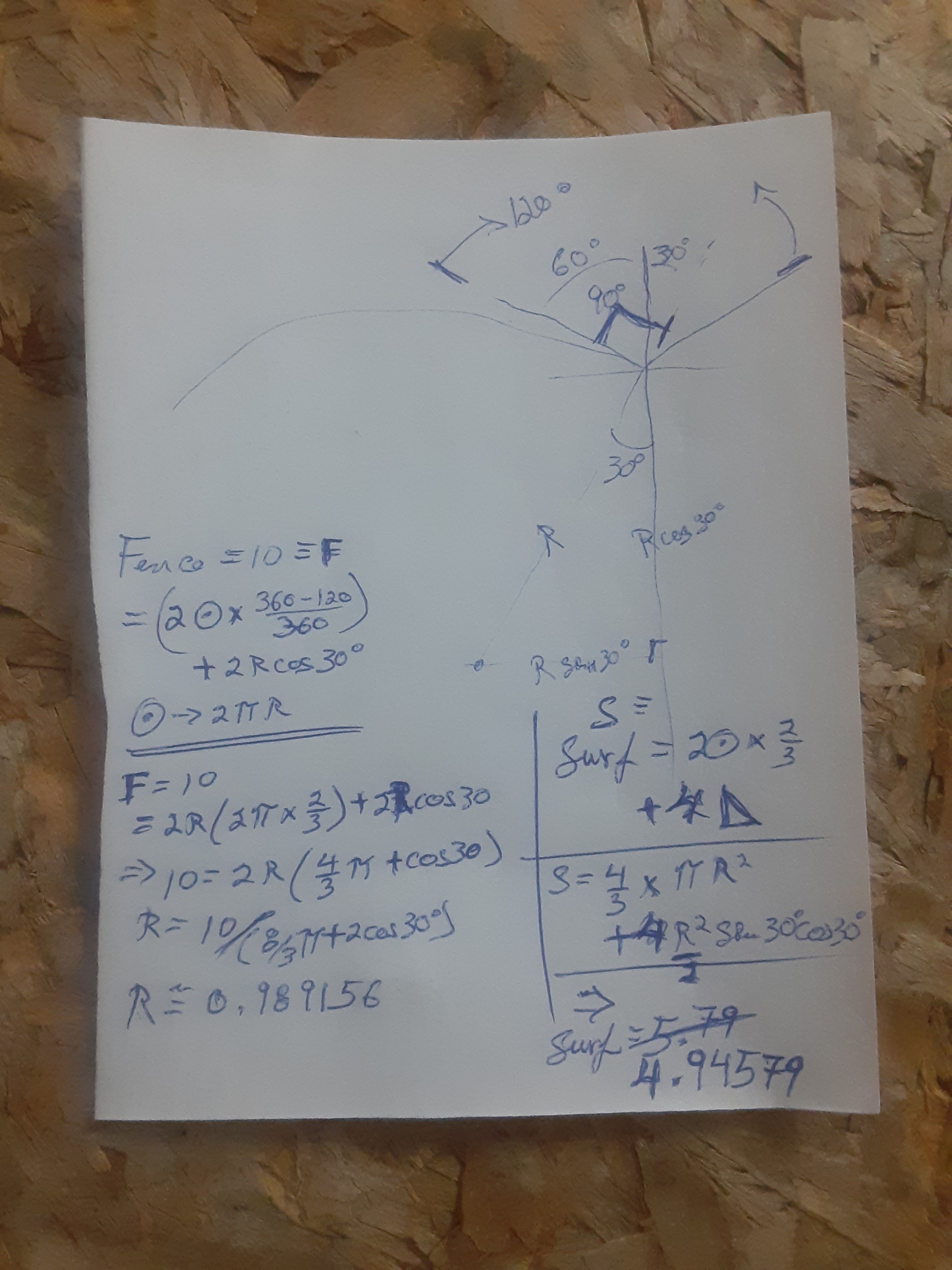
it’s like the shape of two soap bubble touching : at every point where three walls meet there is three times 120°
It looks good, however when I compute the area, I get 4.4872…, which is less than what I get for the single circle. I could be wrong though, as others seem to be getting 4.94.
Edit: I found my mistake! I was using the wrong formula for the altitude of the equilateral triangle. Now I get 4.9458…, which is by far the best result so far. Thank you!

i have the same result, glad for your rabbits (and for you) !
P.S. : You can change the flare to [solved]I’ve implemented a gradient descent algorithm in python to optimize the shape, and I get essentially the same thing:
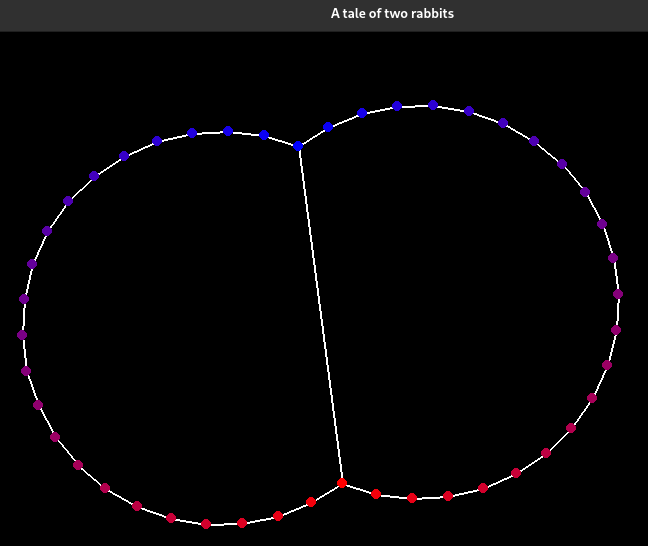
I’m changing the title to solved :)
Here’s the code: https://pastebin.com/wKvhVvQg
You have the best solution so far, but I wouldn’t call it solved yet, since we don’t have any proof or indication that it is the best solution that exists.
Nice Problem you got there. I am not really in a mood to do functional calculus, but this question is a functional calculus question. I will try to give the setup, but not going to solve it (sorry, getting sleepy).
with some clever symmetry arguments, the fence should be symmetric about a line (or plane) bisecting the 2 rabbits, and since we have to also create a wall there, we have to have a line, somewhere in this plane
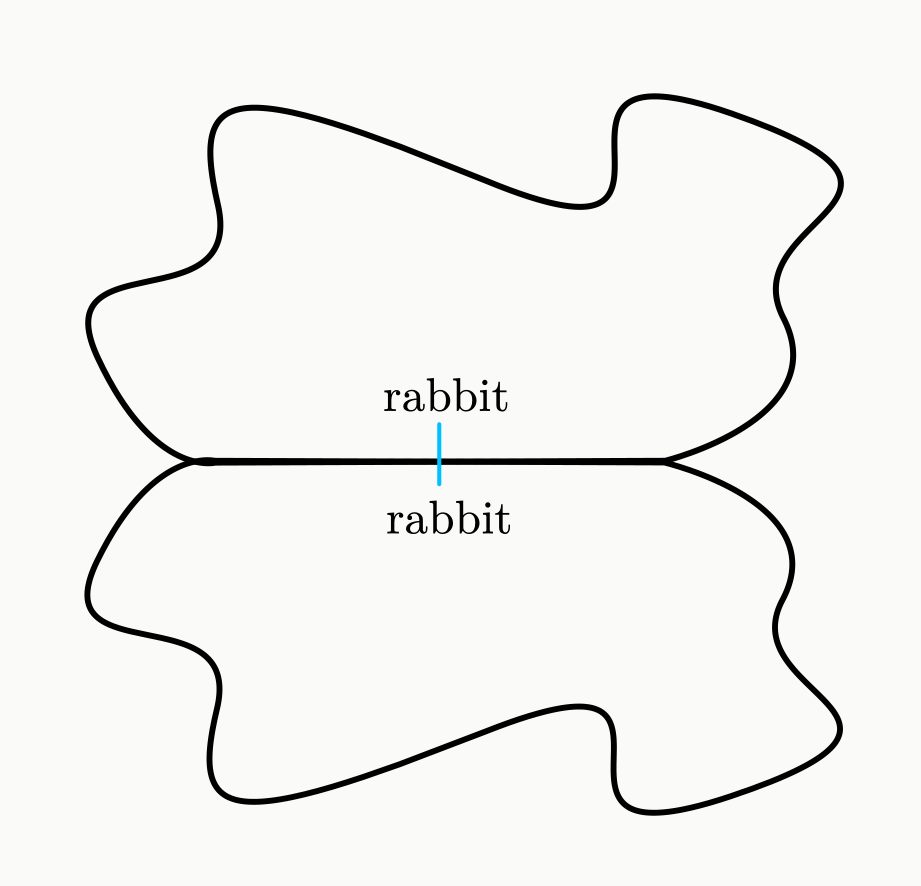
now we can consider a parametric form for equation of fence.
if you are unaware of functional calculus, it is a very fun branch of calculus, where instead of maximising value of a variable, we maximise a “function” it self. for a readup, refer https://en.wikipedia.org/wiki/Action_(physics)#Hamilton’s_characteristic_function https://en.wikipedia.org/wiki/Euler–Lagrange_equation
To solve, we need a constant (or a constraint, in this case total fence length), and a function which we want to extremise (in this case, maximise the area of enclosed by fence).
to keep the problem simple, lets consider, a single valued function (f(x) -> y) (for a general proof, we can do f(x, y) -> z), and also consider some dividing segment, now lets consider the leftmost and rightmost extremes to have values +/- alpha (assuming symmetry in this direction also, not necessary to assume this, but doing for simplicity), now we have a straight fence between some section of these extremes (lets say +/- beta) now total length of fence is constant so
10 = 2 beta + twice (line integral from - alpha to + alpha of f(x))
(line integral is not same as usual integral, you may also know it by name of path integral)
this gives us a constraint
now we can find area enclosed by
twice (integral from - alpha to + alpha f(x) dx )
now use the Euler - Lagrange equation to find a solution for f(x)
this is a very general way to find the solution, and this will also mathematically prove that our solution is the best. If you are also not interested in doing maths, you can use some llm (like chatgpt) to formally setup the problem for you, and then you can use some solver like wolfram alpha to get solution.
Hi, I’m familiar with the concept of Euler-Lagrange equations, however I wouldn’t know how to use them in practice to solve a problem like this one. ChatGPT isn’t very helpful and suggest a single circle cut in half is the optimal solution, even when I tell it to use Euler-Lagrange.
maybe instead of asking it to solve from scratch, just dump in my reply maybe that may help, i am not a expert with prompt engineering. Although, you can find similar problems in standard textbooks. I remember in one of my exams i had basically same problem, but had to minimise area instead.
for usage of euler lagrange, maybe the following may help
https://math.stackexchange.com/questions/346027/satisfy-the-euler-lagrange-equation https://math.stackexchange.com/questions/2337413/find-the-surface-of-least-area-spanned-by-a-given-contour https://www.sas.rochester.edu/mth/undergraduate/honorspaperspdfs/alfredovargas2018.pdf https://math.uchicago.edu/~may/REU2019/REUPapers/Zheng,SiqiClover.pdf https://en.wikipedia.org/wiki/Minimal_surface#History
The best I was personally able to obtain is the circle divided by a wall.
I initially asked this question on the mathematics stack exchange: https://math.stackexchange.com/questions/5035579/area-maximization. Of course, it got closed for no reason, but before it did, someone offered the following solution: join two circular arc (subtended at angle 240∘ with respect to their center) at their end points, add a line segment between the end points, you can achieve an area ∼4.9457788. Recomputing the area of their solution, I get ~4.49 instead, but I’m not sure I got it right…
Please crosspost this on !bunnies@lemmy.world
Does the entire boundary have to be made of the mesh? Especially relevant if this is for practical use rather than just a challenge since you could use e.g. two existing corners in a rectangular yard: cut the mesh in half, and use 5m to close off each corner. Making isosceles triangles out of each corner with the two equal length sides having length sqrt(25/2) ~= 3.535m gives areas of 6.25 sq. meters for each rabbit.
You could do even better if you happened to already have 3 walls of the appropriate lengths to partition off an area in as well… e.g. 2.5m x 5m = 12.5 sq m. for each rabbit if you have a rectangular yard surrounded by an existing wall where the back wall is 5m long and the other two sides are at least 2.5m long. That configuration is less likely for someone to already actually have though.
In my case, yes, because I don’t have much to attach the mesh wire to.
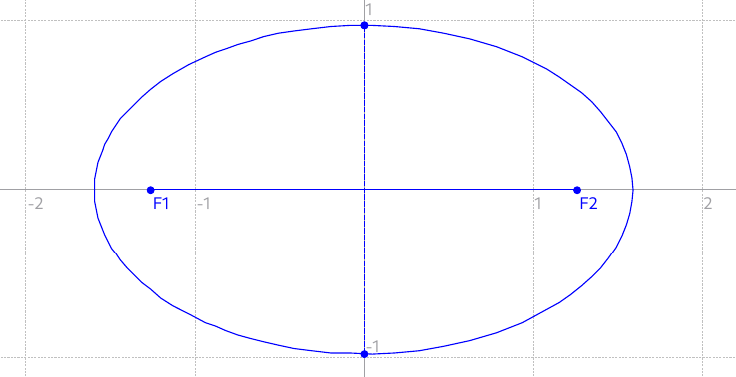
Here’s another solution, that is suboptimal but might be preferable to the soap bubble solution in practice: an ellipse with long axis 1.592 and short axis 0.972. This should be close to the optimal ellipse (I used Kepler’s approximate P=pi * (a+b) formula for the perimeter). It gives an area of 4.861 which is close enough to the current optimum, and looks like this: